Зависимость
туннельного
тока от
расстояния
между зондом
и подложкой
В основе
принципа
работы СТМ
лежит эффект туннелирования
электронов
через узкий потенциальный
барьер между
двумя
проводниками
- зондом и
подложкой -
во внешнем
электрическом
поле.
Рисунок
2
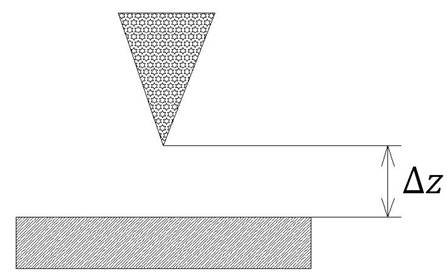
Рисунок
1
В СТМ зонд
подводится к
образцу на
расстояние ![]() порядка
1 Нм (рисунок 1).
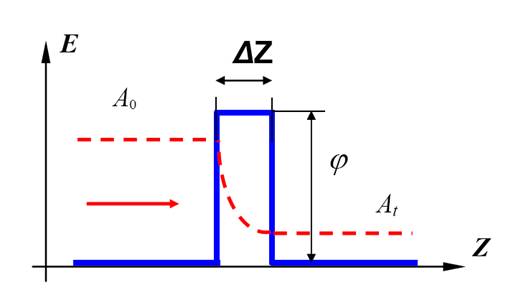
При этом
образуется
потенциальный
барьер (см.
рисунок 2) шириной
порядка
1 Нм (рисунок 1).
При этом
образуется
потенциальный
барьер (см.
рисунок 2) шириной
![]() .
Высота
барьера
определяется
значениями работы
выхода
электронов из
материала
зонда
.
Высота
барьера
определяется
значениями работы
выхода
электронов из
материала
зонда ![]() и
образца
и
образца ![]() . Для
простоты
будем
считать
барьер
прямоугольным
с высотой,
равной
средней
работе выхода:
. Для
простоты
будем
считать
барьер
прямоугольным
с высотой,
равной
средней
работе выхода:
![]() .
.
Для
одномерного
прямоугольного
барьера уравнение
Шредингера
легко
решается, и
можно
вычислить вероятность
туннелирования
как:
![]() , где
, где ![]() .
.
В случае
отсутствия
внешнего
электрического
поля
вероятность
туннелирования
из зонда в
образец
равна
вероятности
туннелирования
из образца в
зонд, и,
следовательно,
средний ток
электронов
равен нулю.
При
приложении
разности
потенциалов V между
зондом и
образцом
появляется
ненулевой
туннельный
ток, который
создается в основном
электронами
с энергией в
окрестности
уровней
Ферми EF1 и EF2 (рисунок
3).
Формула,
выражающая
зависимость
плотности
туннельного
тока, была
получена J.G.Simons’ом в 1963
году: Если
напряжение
мало
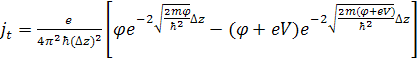 (1)
(1)![]() , выражение
для
плотности
тока можно
представить
в более
простом
виде,
разлагая
вторую экспоненту
в ряд по
, выражение
для
плотности
тока можно
представить
в более
простом
виде,
разлагая
вторую экспоненту
в ряд по ![]() и
пренебрегая
членами с
и
пренебрегая
членами с ![]() Получим:
Получим:![]() (2)
(2)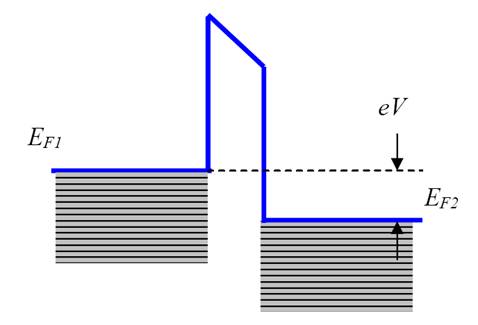
Рисунок
3
энергетическая
диаграмма
туннельного
контакта
двух
металлов
Так как
экспоненциальная
зависимость
сильнее, чем 1/![]() , то для
оценок и качественных
рассуждений
можно
пользоваться
упрощенной
формулой:
, то для
оценок и качественных
рассуждений
можно
пользоваться
упрощенной
формулой:
![]() (3)
(3)
В формуле (3)
величина ![]() считается
независящей
от
считается
независящей
от ![]() . Для
типичной
работы
выхода
. Для
типичной
работы
выхода ![]() значение
константы
затухания k = 2 A-1, так
что при
изменении
значение
константы
затухания k = 2 A-1, так
что при
изменении ![]() на 1
ангстрем
сила тока
меняется на порядок.
на 1
ангстрем
сила тока
меняется на порядок.
Реальный
туннельный
контакт в СТМ
не является
одномерным и
имеет более
сложную геометрию,
однако
основные
черты
туннелирования,
а именно
экспоненциальная
зависимость
тока от
расстояния
зонд-образец,
сохраняются
также и в
более сложных
моделях, что
подтверждается
экспериментально.
Для больших
напряжений ![]() из
формулы (1)
получается формула
Фаулера-Нордгейма
для полевой
эмиссии
электронов в
вакуум:
из
формулы (1)
получается формула
Фаулера-Нордгейма
для полевой
эмиссии
электронов в
вакуум:
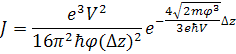
Экспоненциальная
зависимость
туннельного
тока от
расстояния (3)
позволяет
осуществлять
регулирование
расстояния
между зондом
и образцом в
туннельном
микроскопе с
высокой
точностью.